RWKVにおけるwkv構造

前回のブログで，RWKVのattentionに相当する構造であるwkvが，GPT modeとRNN modeの二つの方法で計算できることを示しました．

一方で，そもそもwkvの式がどういう経緯でattention相当であるのかは，かなり疑問だったので，自分なりの理解を残しておきます．

Transformerのattentionからwkvまで

ざっくりとしたTransformerからRWKV(GPT mode)への流れは以下に示すオレンジ色の通りです．青色は前回のブログで示した関係です．

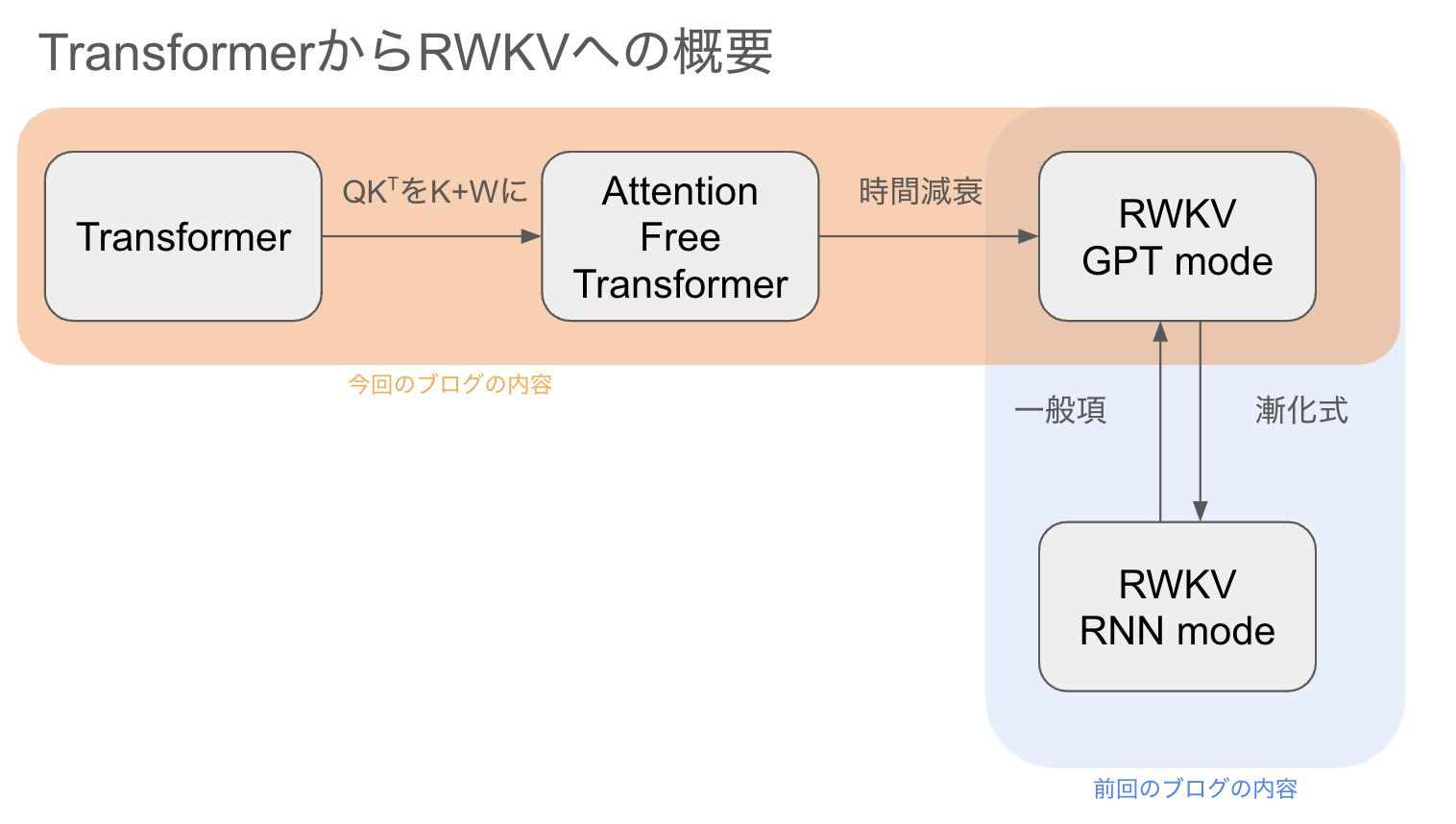
Transformer→Attention Free Transformer

Transformerにおける自Attentionの計算は以下の通り．（dは隠れ層の次元，Tはトークン列長）
$$
Q,K,V\in \mathbb{R}^{T\times d}
$$

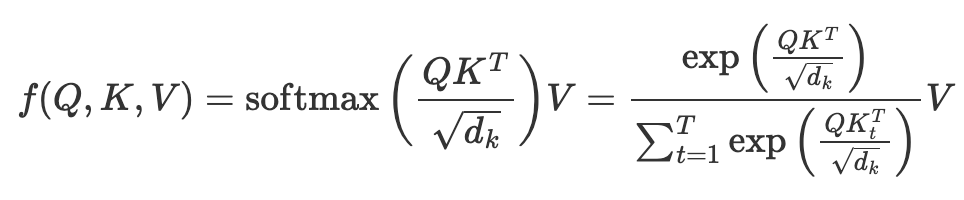
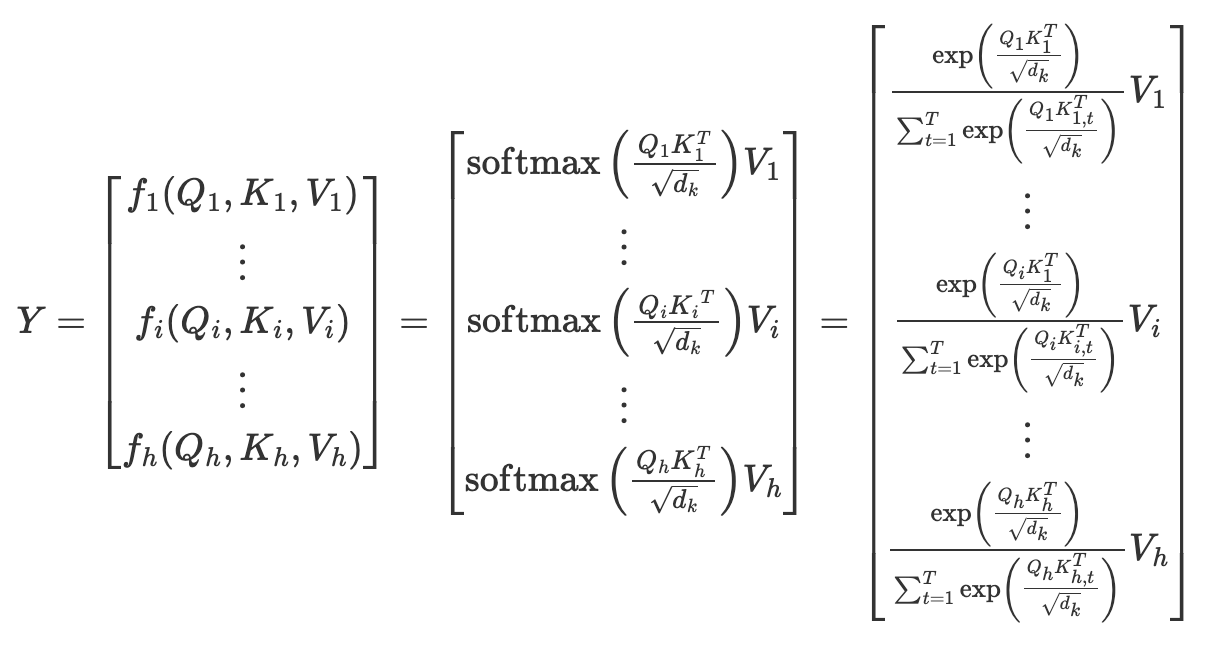
Transformerではこれをheadの数だけ並列して行うMulti-Head Attentionという計算をしています．従って，先の式をheadの数hだけ，1〜hを並べると，以下のようになります．YがMulti-Head Attentionの出力になります．
$$
Y \in \mathbb{R}^{h\times d\times T}
$$

Attention Free Transformerではここで以下のような変更を加えます．

  • headの数をhを次元数dにして，V1〜VhをV1〜Vdにする（Multi-Head Attentionの出力がd次元なので，その後のConcatenate層でhd次元をd次元にに揃える必要がなくなる）
  • 出力Ytの各次元の成分は，入力VtとAttentionベクトルa_t^dの内積をとったものである．

これをもとに先の式を書き換えると，ある時刻t(1≦t≦T)の出力Ytは

$$
Y \in \mathbb{R}^{d\times T},\mathbf{a}_t^i \in \mathbb{R}^{d}
$$

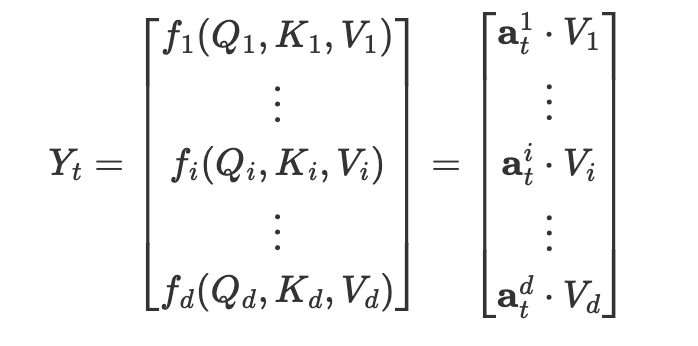
加えて，アテンションベクトルa_t^d は行列積QK^Tではなく，Queryとの要素積と，Keyに対するトークンの相対位置バイアスWで計算します．これに伴い，分母の√dは行列積に対するスケーリングであったため消えます．

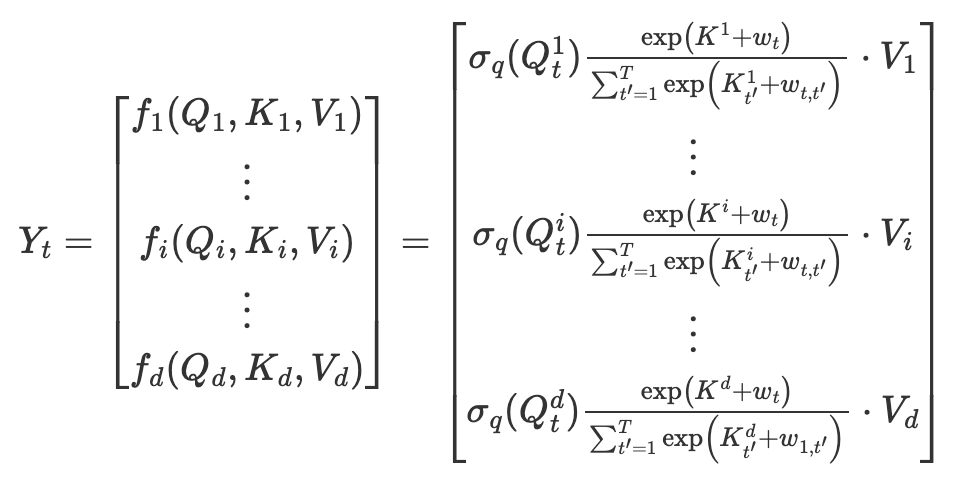
続いて，Ytは入力VのAttentionの重みの平均と考えて（分子にもΣがつく），Ytをトークンの数Tだけ並べると，次の式になります．Multi-Head Attentionに似た式が出てくると思いますが，行列の要素積と和のみの計算のため，(空間)計算量はシーケンス長Tに対して線形で済みます．

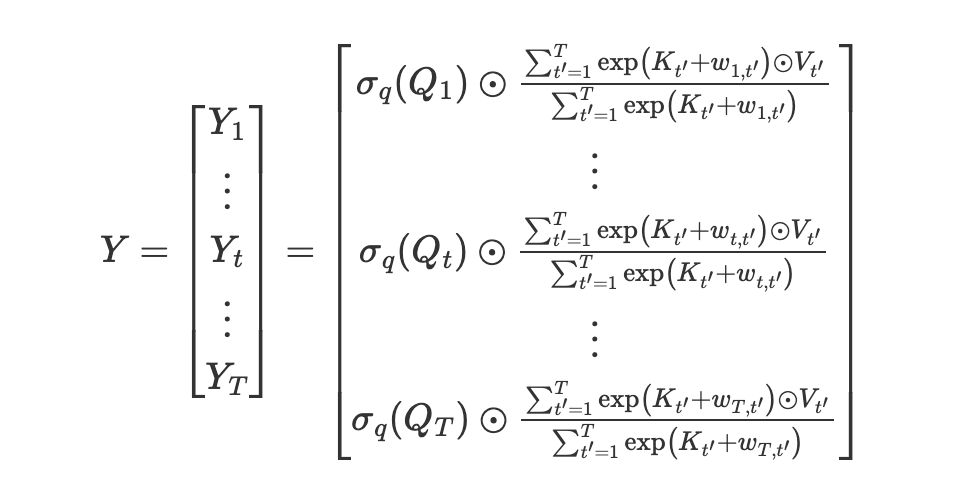
Attention Free Transformer→RWKV

先のYをwkvの式に変形します．

あるAttention Free Transformer(AFT)のAttentionのtにおける出力は先の式より
$$
Y_t=\sigma_q(Q_t) \odot \frac{\sum_{t’=1}^T \exp(K_{t’} + w_{t,t’}) \odot V_{t’}}{\sum_{t’=1}^T \exp(K_{t’} + w_{t,t’})}
$$

これに時間減衰を導入します．分子がValueの重みつき平均であったのを，自身のトークンtに対して，直前のトークン(t-1)までのValueを，トークン数に比例して重み（バイアス項W）を減少させます．自身の時刻tから遠いトークンほど，Valueの平均への影響が小さくなるイメージです．

$$
Y_t=\sigma_q(Q_t) \odot \frac{\sum_{t’=1}^{t} \exp(K_{t’} + (i-t)w_{t,t’}) \odot V_{t’}}{\sum_{t’=1}^{t} \exp(K_{t’} + (i-t)w_{t,t’})}
$$

最後に，Queryを情報の受け入れ(Receptance)と考えてRとおき，位置バイアスwを時刻tとそれ以前の重みu,wに分ければ，RWKVにおける時刻tのwkvの式が出てくる．

$$
Y_t=\sigma_q(R_t) \odot \frac{\sum_{t’=1}^{t-1} \exp(K_{t’} + (i-t+1)w) \odot V_{t’}+ \exp(K_{t} + u)\odot V_t}{\sum_{t’=1}^{t-1} \exp(K_{t’} + (i-t+1)w)+ \exp(K_{t} + u)}=\sigma(r_t)\odot wkv_t
$$

以上，TransformerのAttention(Q,K,V)から，RWKVの名前にあるようにR,W,K,Vが見えました．

最後に

RWKVは，あくまで”TransformerをRNNにしたもの”ではなく，”AFTをRNNにしたもの”なので，wkv構造だけの性能ではAFTが上限になる気がします．RWKVにはwkv以外にもchannel mixingやToken shiftなどが実装されており，wkv構造単体に関するablation実験がされておらず，その点は現在性能はよくわかっておりません．同じくRecurrent modeとParallel modeが使い分けれるRetNetの論文でも同様の話がされており，こちらではフェアな評価のため，Attention層をTime mixing層と入れ替えたもののみで比較（§3.5）しており，Language modelingではそれなりに低いperplexityを出しています（Table 5）．

2023/11現在，LLMのローカルマシンで動作させる場合，計算精度を4bit程度に落とすことが主流ですが，RetNetやRWKVのように学習と推論で計算量が異なる計算を行う方法が進むことに個人的に期待しています．

誤り等ありましたら，@gojitejiまでご連絡ください．

参考文献